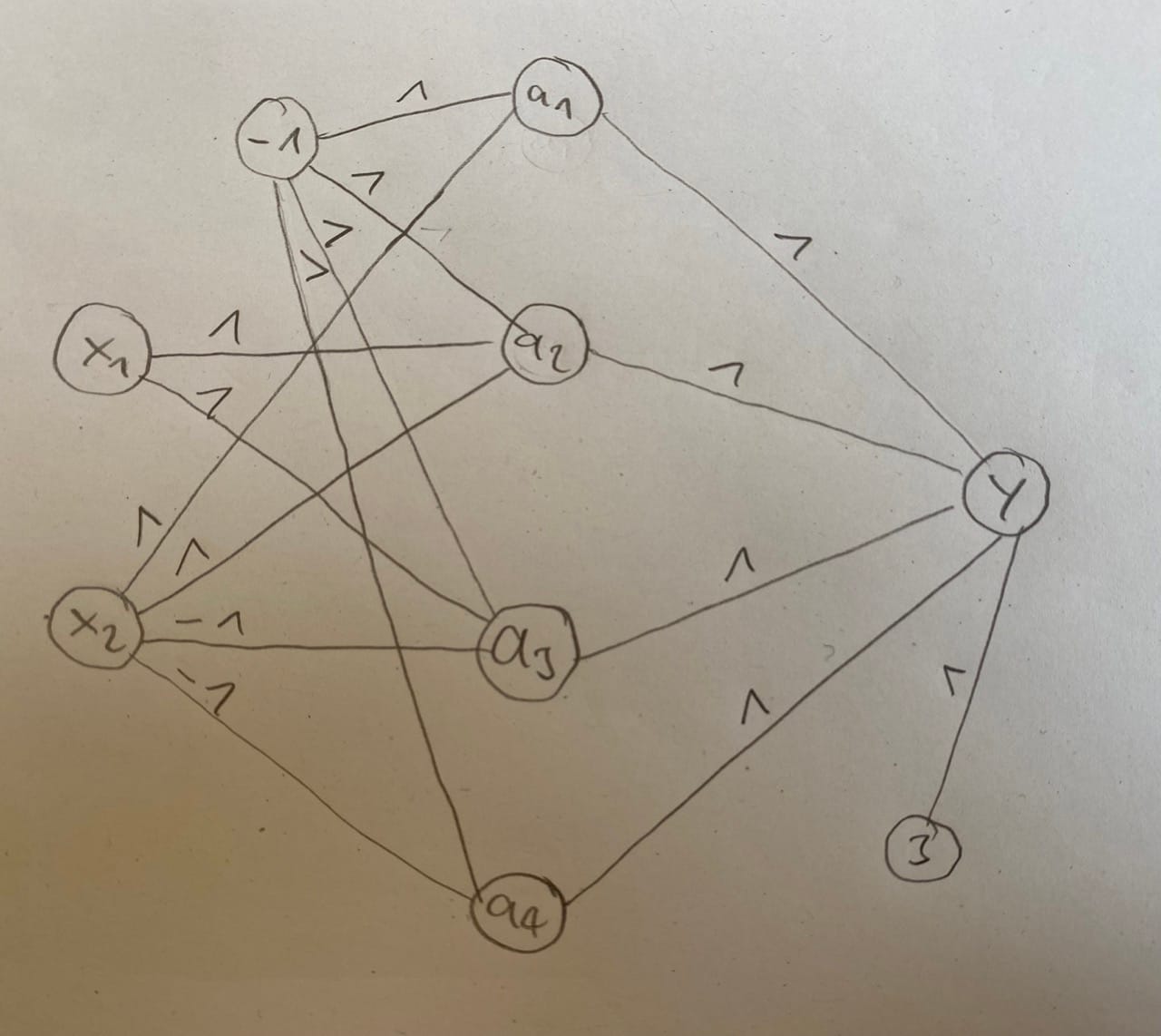
Manual design of a Neural Net

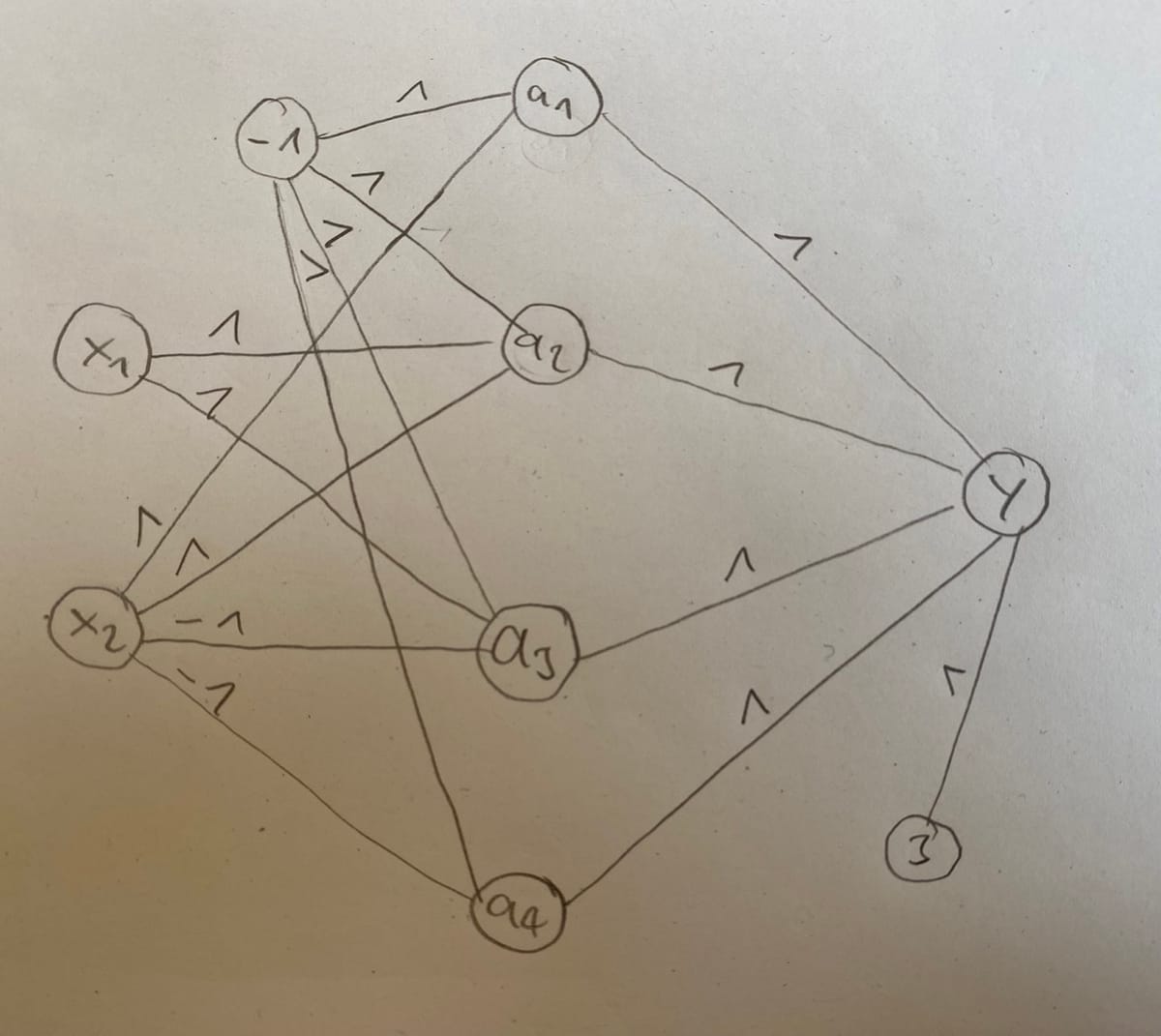
The following is a typical homework and exam task in Machine Learning 1 and Deep Learning 1 at TU Berlin.

The Task

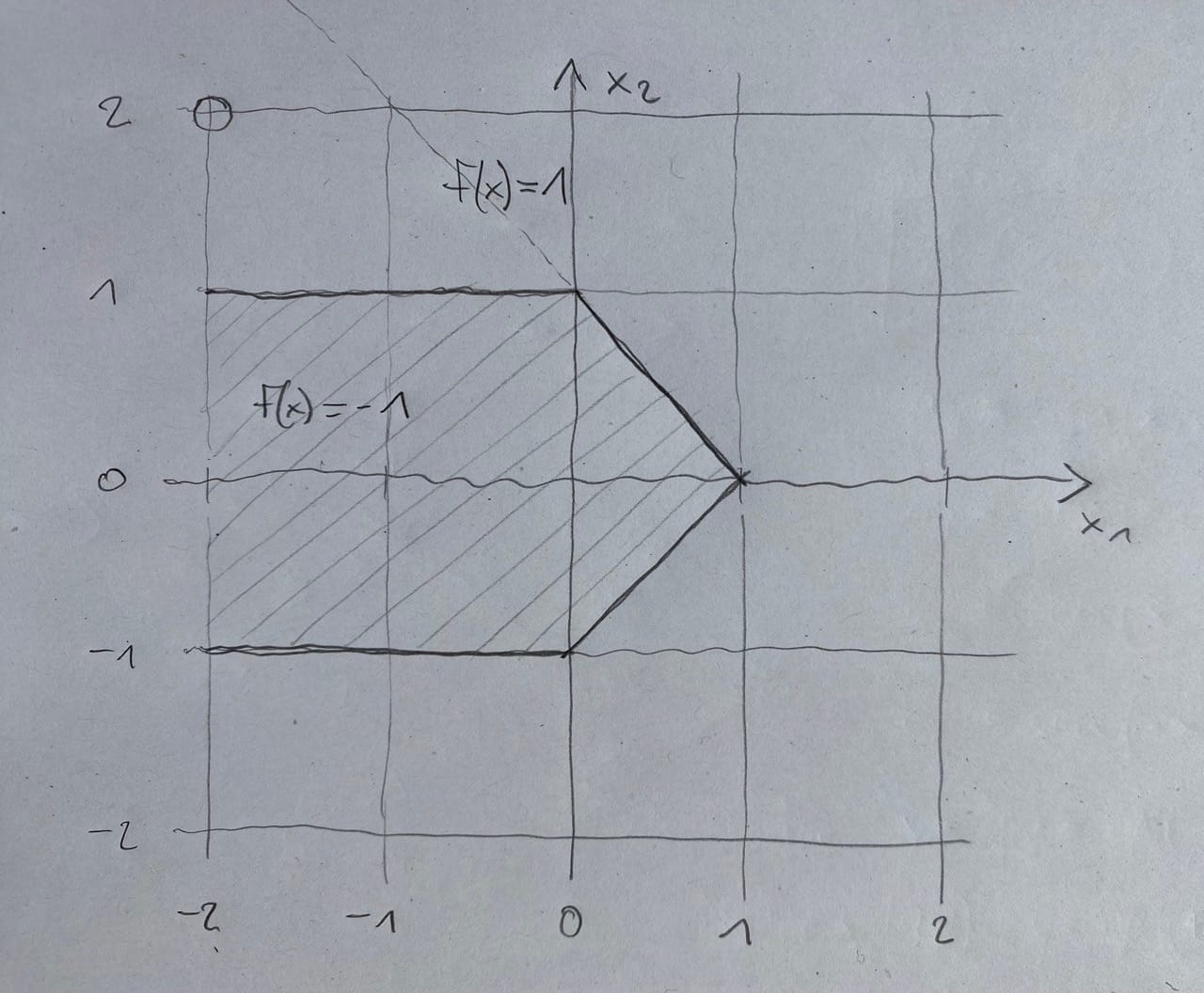
Below you see the desired output of a simple Neural Network, represented by the shaded \(f(x)= -1\) and non shaded areas \(f(x)= 1\). Further we see a test point at \(x= (-2,2)\) indicated with which we should verify as the output of our Neural Net.

Solution

We see that the input of this network is dependent on 2 inputs, \(x_1\) and \(x_2\) as every point in 2d space is dependent on these variables.

We can also see, that the 2 areas are separated by 4 linear boundaries. The general equation for these boundaries (\(w\) being the weights and \(b\) being the bias) is given by:

\[ f(x) = w_1x_1 + w_2x_2 + b\]

Boundary equations

Let's go ahead and write down the specific boundary equations, going from the horizontal line top left clockwise. Then we also reorder them, so they equal to 0 and take the sign function as an activation, which returns if the argument is negative of positive.

\[ \begin{array}{llll} \text{Boundary 1 :} & \text{Boundary 2 :} \\ x_2 = 1 & x_2 = -x_1 + 1 \\ x_2 - 1 = 0 & x_2 +x_1 - 1 = 0 \\ a_1 = \text{sign} (x_2 - 1) & a_2 = \text{sign} (x_2 +x_1 - 1) \\ & \\\text{Boundary 3 :} & \text{Boundary 4 :} \\ x_2 = x_1 - 1 & x_2 = - 1 \\ x_2 - x_1 + 1 = 0 & x_2 + 1 = 0 \\ a_3 = \text{sign} (x_2 - x_1 + 1) & a_4 = \text{sign} (x_2 + 1) \end{array} \]

Adjusting for correct activation

So far so good. Now we need to check if every equation gives us the correct output when inserting values for \(x_1\) and \(x_2\). If the output is not the desired one, we need to flip the signs of our equation. Easiest seems to plug \(x_{1,2}= (0,0)\). As a result we should get -1.

\[ \begin{array}{ll} \text{Boundary 1 :} & \text{Boundary 2 :} \\ a_1 = \text{sign} (0 - 1) = -1 & a_2 = \text{sign} (0 +0 - 1) = -1 \\ & \\ \text{Boundary 3 :} & \text{Boundary 4 :} \\ a_3 = \text{sign} (0 - 0 + 1) = \color{red}1\color{black} & a_4 = \text{sign} (0 + 1) = \color{red}1\color{black} \end{array} \]

So Boundaries 1 and 2 are ok, but Boundaries 3 and 4 need to flip signs to yield the correct class:

\[ \begin{array}{ll} \text{Boundary 1 :} & \text{Boundary 2 :} \\ a_1 = \text{sign} (x_2 - 1) & a_2 = \text{sign} (x_2 + x_1 - 1) \\ & \\ \text{Boundary 3 :} & \text{Boundary 4 :} \\ a_3 = \text{sign} (-x_2 + x_1 - 1) & a_4 = \text{sign} (-x_2 - 1) \end{array} \]

Output layer

These 4 boundary equations are the activations for the 4 neurons on the hidden layer of our neural network. Finally these 4 neurons are connected in the final layer which follows the same principle.

\[ y = \text{sign} \left ( \sum_{i=1}^{4} w_{i1}x_1 + w_{i2}x_2 + b_i \right )\]

Now, if we insert the test point \(x= (-2,2)\) into our 4 activation functions we get:

\[ \begin{split} y &= \text{sign} \left ( +1 -1 -1 -1\right )\\ &= \color{red}-1\color{black} \end{split}\]

This is not correct, we see that just boundary 1 correctly identifies the class as 1, the other three boundaries as -1. We can fix this by introducing a bias of \( +3 \) in the output neuron which requires all 4 hidden neuron activations to be \( -1 \) in order to yield a an output of \( -1 \).

\[ \begin{split} y &= \text{sign} \left ( \left (\sum_{i=1}^{4} w_{i1}x_1 + w_{i2}x_2 + b_i \right ) + b \right ) \\&= \text{sign} \left ( (+1 -1 -1 -1) + 3\right )\\ &= 1 \end{split}\]

So now we get the correct result for our test point \(x= (-2,2)\)

Network visualisation